L’élève aveugle :
- vit dans un monde en 3 D uniquement (seule la vue permet de percevoir et de comprendre l’espace en 2 D)
- ne peut écrire que linéairement, avec des caractères qui font tous la même taille et sont tous situés sur une même ligne.
Pour lui, la géométrie est cruciale, il doit la maîtriser aussi pour gérer ses propres déplacements dans l’espace.
Les vidéos présentées sont extraites du reportage « qui a peur des maths ? » (émission « à vous de voir » sur France 5) à revoir ici.
Contrainte linéaire
Avec l’aide de Sandrine Boissel, enseignante spécialisée
En braille, le texte ne peut être que linéaire. Fractions, exposants, fractions de fractions… les équations mathématiques, développées sur une seule ligne, sans indices visuels, sans vision globale, demandent une concentration sans faille.
Le braille informatique permet de saisir les formules en braille et d’obtenir une impression respectant les règles de présentation classique, avec tous les attributs nécessaires. Mais cela nécessite d’ajouter à la formule des indicateurs supplémentaires.
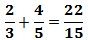
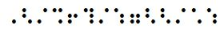
`’2/3!4/5″22/15 `’ê/î!ô/û »êê/âû Numérateurs et dénominateurs se succèdent, impossible de repérer immédiatement, en se basant sur les éléments sur/sous la barre de fraction, un dénominateur commun. Impossible de simplifier en rayant.
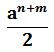
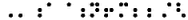
`’„a^„n!m;;/2 `’„a^„n!m;;/ê Voir ici les ambiguïtés possibles quand la formule est dictée oralement.
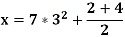
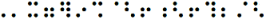
`’x »7*3^2!„2!4;/2 `’x »ï*î^ê!„ê!ô;/ê Pour être plus précis, nous utilisons la table Keyboard alt codes braille : (alt 096)’ x »7*3^2!(alt 0132)2!4;/2
Dans certains cas qu’il n’est pas évident de maîtriser, l’élève doit ajouter certain signes (comme des parenthèses, des « début de bloc » et « fin de bloc », des signes de passages du littéraire aux maths, etc…) pour que sa formule puisse être correctement imprimée. Certaines erreurs dans l’utilisation de ces signes empêchent l’impression ou font que tout ce que l’élève a écrit lui apparaît comme normal à la lecture sur son ordinateur mais disparaît à l’impression (sans laisser de vides pour autant, juste comme si l’élève n’avait pas fait tout ou partie de l’exercice), ce qui est source de quiproquo.
— > Par sécurité, lors des contrôles, on peut récupérer aussi le travail sous clé USB de façon à vérifier en cas de doute après correction, en lisant le fichier sur l’écran de l’ordinateur de l’élève, s’il y avait bien ou non quelque chose d’écrit.
La lecture de grandes formules devient très vite fastidieuse, d’autant plus qu’elle tient souvent sur plusieurs lignes.
L’enseignement des mathématiques à des élèves déficients visuels.
Les bases sont expliquées ici
Un lycéen aveugle explique comment il a eu le « déclic » en visualisant mentalement les opérations sur plusieurs lignes :
Géométrie concrète
La démonstration en volume, par manipulation, pliages, puzzles… permet de beaucoup mieux intégrer les règles géométriques que les schémas à plat, même retranscrits en relief.
Sommes des angles d’un triangle
CQFD !
Pythagore
ReCQFD !
Ci-dessous le mode d’emploi d’un puzzle réalisé par Jean Meyer puis adapté tactilement.
Cube développé
Mieux que le découpage/pliage :
Géométrie en 3D
Utile aussi bien pour les élèves voyants…
Utilisation du pliage/origami
à lire
- Apprendre en jouant grâce au Tangram
- Les mathématiques de l’Origami et la comparaison avec les constructions à la règle et au compas
à voir
- Origami et mathématiques : http://www.irem.univ-paris-diderot.fr/videos/origami_et_mathematiques/
- Apprendre les maths par le pliage
Matériel spécialisé
Planche à dessiner
Permet d’effectuer des dessins géométriques grâce à son système de règles coulissantes sur rails.
Outils de géométrie
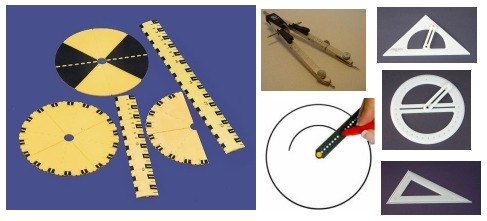
Règles, rapporteurs, mais aussi équerres, compas… existent avec marques tactiles
Sur les règles, équerres, rapporteurs…, les graduations en relief sont précises au demi-centimètre ou au 5°, ce qui est déjà difficile à percevoir tactilement.
Vidéos
Figures géométriques
Ensemble de figures géométriques planes.
Sur la photo :
- 2 rectangles avec diagonales
- 2 carrés avec diagonales
- 3 triangles avec hauteurs
- isocèle
- rectangle
- équilatéral
- 4 cercles avec diamètre, rayon, secteur et arc
- 2 trapèzes isocèles avec diagonales et hauteurs
- 1 trapèze rectangle avec hauteur
- 2 losanges avec diagonales
- 2 pentagones avec diagonales et hauteur
- 2 hexagones avec diagonales et hauteur
Sur chaque figure est représentée, par une ligne esquissée en pointillés (relief, hauteur, rayon ou diagonale).
Support de géométrie avec abscisses et ordonnées
Pour démontrer les concepts géométriques, introduire les noms des formes, travailler sur les aires, sur la symétrie, représenter les fractions… à l’aide d’élastiques qui se fixent autour des picots du tableau. Le problème des supports classiques est qu’il est impossible de noter les noms des points. Voici une adaptation pour y remédier :
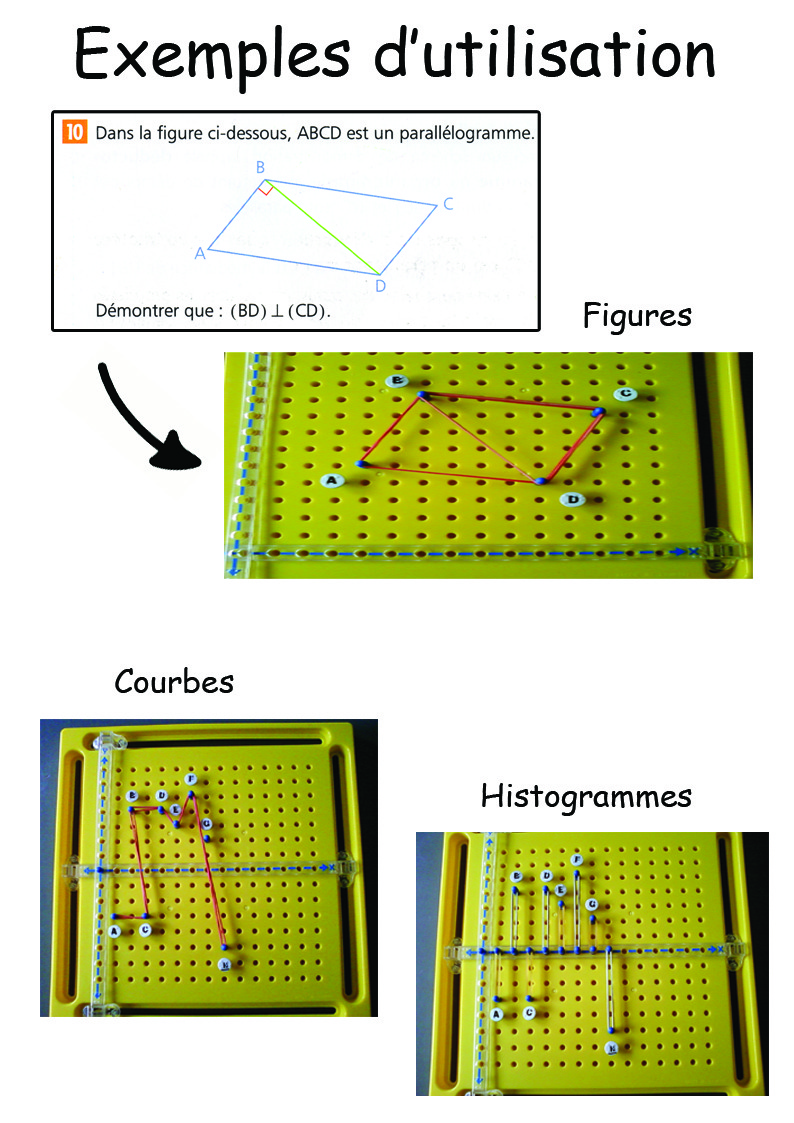
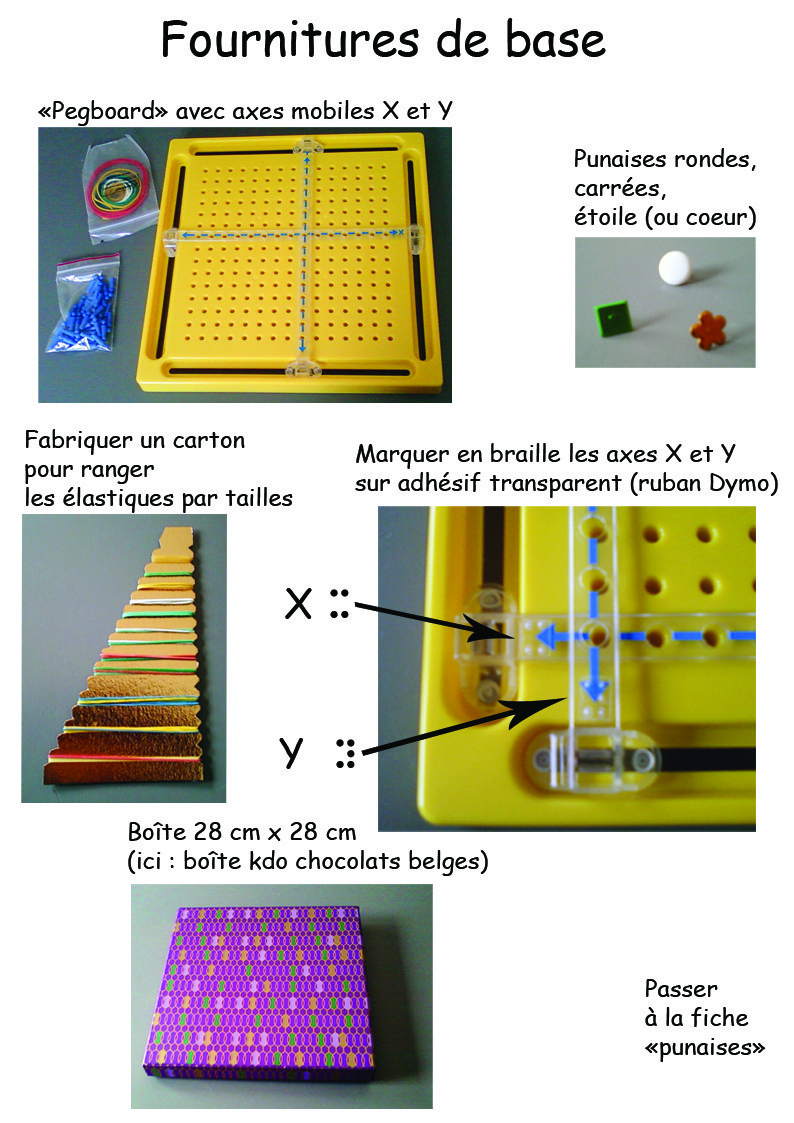
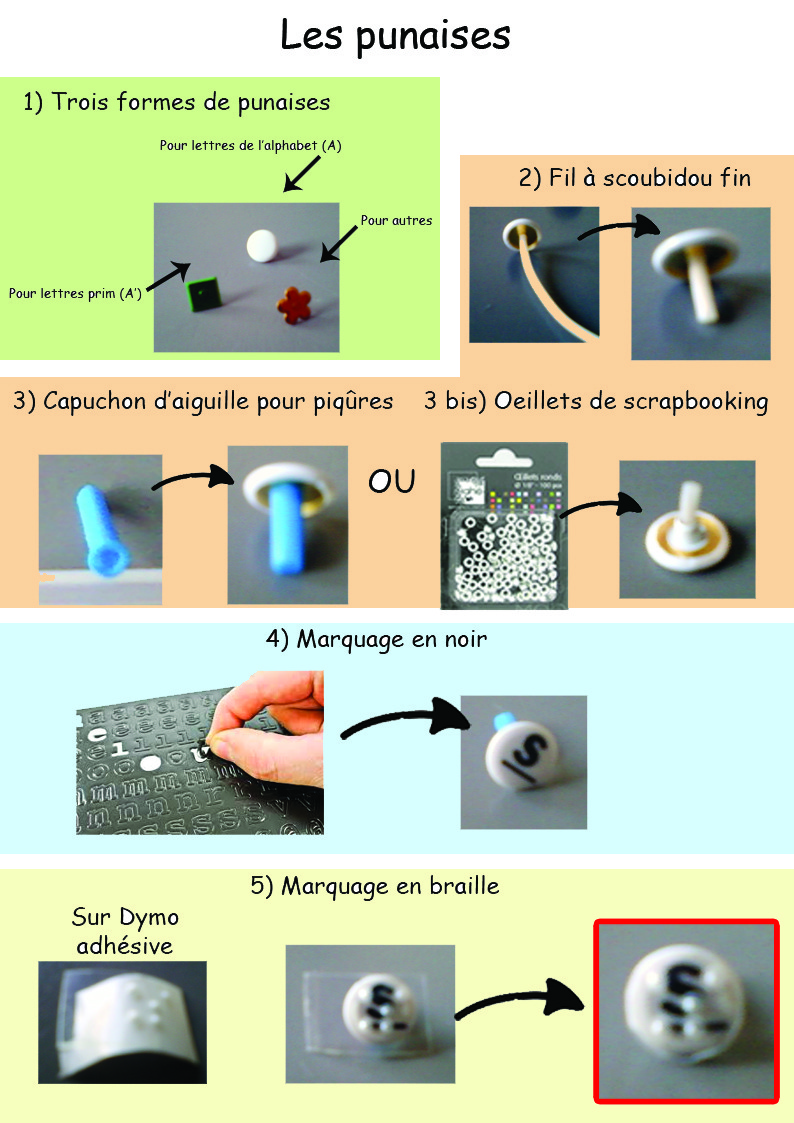
Variante de rangement des points avec un morceau de grille de Coloredo :
Support de géométrie version junior
Il existe des formes adaptables sur ces tableaux.
Calcul
Avant le collège, voir ici
Calculette parlante
Il existe des calculettes vocalisées, à écouter avec un écouteur mono-oreille.
Calculatrice électronique
Les ordinateurs braille possèdent une fonction calculatrice (option simple ou scientifique).
Calcul graphique
Il n’existe pas de calculatrices scientifiques graphiques adaptées à la cécité.